Шишков И.А. и др. Сооружени...
подробнее
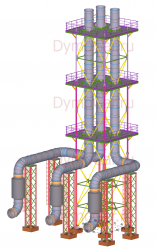
Каждая дымовая труба для котельной или промышленного предприятия разрабатывается в индивидуальном порядке с учетом специфики производства, состава отводимых газов и климатических особенностей района строительства.
Расчет, как правило, выполняется с помощью проектно-вычислительного комплекса, таких как SCAD, ЛИРА-САПР, Robot Structural Analysis, IDEA StatiCa, STAAD, APM Structure3D. Комплекс реализует конечно-элементное моделирование статических и динамических расчетных схем, проверку устойчивости, выбор невыгодных сочетаний усилий, подбор арматуры железобетонных конструкций, проверку несущей способности стальных конструкций. В представленной ниже статье описаны лишь фактически использованные при расчетах дымовых труб возможности комплексов.






В основу расчета положен метод конечных элементов с использованием в качестве основных неизвестных перемещений и поворотов узлов расчетной схемы. В связи с этим идеализация конструкции выполнена в форме, приспособленной к использованию этого метода, а именно: система представлена в виде набора тел стандартного типа (стержней, пластин, оболочек и т.д.), называемых конечными элементами и присоединенных к узлам.
Тип конечного элемента определяется его геометрической формой, правилами, определяющими зависимость между перемещениями узлов конечного элемента и узлов системы, физическим законом, определяющим зависимость между внутренними усилиями и внутренними перемещениями, и набором параметров (жесткостей), входящих в описание этого закона и др.
Узел в расчетной схеме метода перемещений представляется в виде абсолютно жесткого тела исчезающе малых размеров. Положение узла в пространстве при деформациях системы определяется координатами центра и углами поворота трех осей, жестко связанных с узлом. Узел представлен как объект, обладающий шестью степенями свободы - тремя линейными смещениями и тремя углами поворота.
Все узлы и элементы расчетной схемы нумеруются. Номера, присвоенные им, следует трактовать только, как имена, которые позволяют делать необходимые ссылки.
Основная система метода перемещений выбирается путем наложения в каждом узле всех связей, запрещающих любые узловые перемещения. Условия равенства нулю усилий в этих связях представляют собой разрешающие уравнения равновесия, а смещения указанных связей - основные неизвестные методы перемещений.
В общем случае в пространственных конструкциях в узле могут присутствовать все шесть перемещений:
1 - линейное перемещение вдоль оси X;
2 - линейное перемещение вдоль оси Y;
3 - линейное перемещение вдоль оси Z;
4 - угол поворота с вектором вдоль оси X (поворот вокруг оси X);
5 - угол поворота с вектором вдоль оси Y (поворот вокруг оси Y);
6 - угол поворота с вектором вдоль оси Z (поворот вокруг оси Z).
Нумерация перемещений в узле (степеней свободы), представленная выше, используется далее всюду без специальных оговорок, а также используются соответственно обозначения X, Y, Z, UX, UY и UZ для обозначения величин соответствующих линейных перемещений и углов поворота.
В соответствии с идеологией метода конечных элементов, истинная форма поля перемещений внутри элемента (за исключением элементов стержневого типа) приближенно представлена различными упрощенными зависимостями. При этом погрешность в определении напряжений и деформаций имеет порядок (h/L) k, где h - максимальный шаг сетки; L - характерный размер области. Скорость уменьшения ошибки приближенного результата (скорость сходимости) определяется показателем степени k, который имеет разное значение для перемещений и различных компонент внутренних усилий (напряжений).Для задания данных о расчетной схеме могут быть использованы различные системы координат, которые в дальнейшем преобразуются в декартовы. В дальнейшем для описания расчетной схемы используются следующие декартовы системы координат:
Глобальная правосторонняя система координат XYZ, связанная с расчетной схемой
Локальные правосторонние системы координат, связанные с каждым конечным элементом.
Расчетная схема определена как система с признаком 5. Это означает, что рассматривается система общего вида, деформации которой и ее основные неизвестные представлены линейными перемещениями узловых точек вдоль осей X, Y, Z и поворотами вокруг этих осей.
Расчетная схема характеризуется следующими параметрами:
- количество узлов.
- количество конечных элементов.
- общее количество неизвестных перемещений и поворотов.
- количество загружений.
- количество комбинаций загружений.
Статический расчет системы выполняется в линейной постановке.
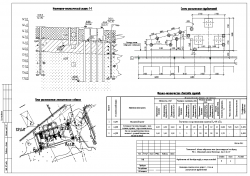
Детальное описание расчетной схемы дымовой трубы должны быть представлены в табличной форме - сведения о расчетной схеме, содержащие координаты всех узлов, характеристики всех конечных элементов, условия примыкания конечных элементов к узлам и др.
Возможные перемещения узлов конечно-элементной расчетной схемы ограничены внешними связями, запрещающими некоторые из этих перемещений. Наличие таких связей помечено в таблице "Координаты и связи" описания исходных данных символом #.
Точки примыкания конечного элемента к узлам (концевые сечения элементов) имеют одинаковые перемещения с указанными узлами.
Исключение составляют стержневые элементы для которых предусмотрено наличие шарниров и/или ползунов, разрешающих угловые и/или линейные перемещения узлов и концевых сечений элементов относительно узлов расчетной схемы.
В расчетную схему дымовой трубы включены конечные элементы следующих типов:
Стержневые конечные элементы, для которых предусмотрена работа по обычным правилам сопротивления материалов. Описание их напряженного состояния связано с местной системой координат, у которой ось X1 ориентирована вдоль стержня, а оси Y1 и Z1 - вдоль главных осей инерции поперечного сечения.
Некоторые стержни присоединены к узлам через абсолютно жесткие вставки, с помощью которых учитываются эксцентриситеты узловых примыканий. Тогда ось X1 ориентирована вдоль упругой части стержня, а оси Y1 и Z1 - вдоль главных осей инерции поперечного сечения упругой части стержня.
К стержневым конечным элементам рассматриваемой расчетной схемы относятся следующие типы элементов:
Элемент, который работает по пространственной схеме и воспринимает продольную силу N, изгибающие моменты Мy и Mz, поперечные силы Qz и Qy, а также крутящий момент Mk.
Конечные элементы оболочек, геометрическая форма которых на малом участке элемента является плоской (она образуют многогранник, вписанный в действительную криволинейную форму срединной поверхности оболочки). Для этих элементов, в соответствии с идеологией метода конечных элементов, истинная форма перемещений внутри элемента приближенно представлена упрощенными зависимостями. Описание их напряженного состояния связано с местной системой координат, у которой оси X1 и Y1 расположены в плоскости элемента и ось Х1 направлена от первого узла ко второму, а ось Z1 ортогональна поверхности элемента.
Треугольный элемент, не является совместным и моделирует поле нормальных перемещений внутри элемента полиномом 4 степени, а поле тангенциальных перемещений полиномом первой степени. Располагается в пространстве произвольным образом.
Четырехугольный элемент, который имеет четыре узловые точки, не является совместным и моделирует поле нормальных перемещений внутри элемента полиномом 3 степени, а поле тангенциальных перемещений неполным полиномом 2 степени. Располагается в пространстве произвольным образом.
Конструкция должна быть рассчитана на статические и динамические загружения.
Динамический расчет системы выполняется с использованием разложения по формам собственных колебаний. При этом в расчете использование не более, чем приведенное ниже число форм:
пульсация ветрового потока по СНиП 2.01.07-85* - 6 форм
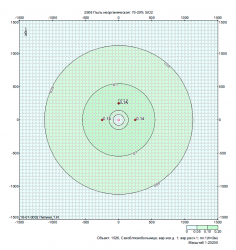
В динамическом нагружении «Пульсация ветрового потока по СНиП 2.01.07-85*» выполняется расчет по методике, в которой давление ветра на сооружение рассматривается как сумма статической и пульсационной составляющих ветровой нагрузки. Последняя есть случайная функция времени, обусловленная случайной скоростью пульсаций. Усилия в элементах системы и перемещения ее точек (обобщенно - реакция сооружения Х) находятся раздельно от статической составляющей ветровой нагрузки и от инерционных сил, соответствующих каждой форме собственных колебаний. Суммарное значение реакции определяется по формуле
из которой видно, что колебания совершаются вокруг смещенного состояния равновесия, соответствующего статической (средней) компоненте нагружения. В результатах расчета представляются отдельные составляющие динамической реакции Xid и суммарное значение статической и всех динамических компонент. При этом знак динамической добавки принимается таким же, как и у компоненты X c.
В отчете результаты расчета представляются выборочно. Вся полученная в результате расчета информация должна хранится в электронном виде.
Вычисленные значения линейных перемещений и поворотов узлов от загружений представляются в таблице результатов расчета «Перемещения узлов».
Вычисленные значения линейных перемещений и поворотов узлов от комбинаций загружений представляются в таблице результатов расчета «Перемещения узлов от комбинаций».
Правило знаков для перемещений принято таким, что линейные перемещения положительны, если они направлены в сторону возрастания соответствующей координаты, а углы поворота положительны, если они соответствуют правилу правого винта (при взгляде от конца соответствующей оси к ее началу движение происходит против часовой стрелки).
Вычисленные значения усилий и напряжений в элементах от загружений представляются в таблице результатов расчета дымовой трубы «Усилия/напряжения элементов».
Вычисленные значения усилий и напряжений в элементах от комбинаций загружений представляются в таблице результатов расчета «Усилия/напряжения элементов от комбинаций загружений».
Для стержневых элементов усилия по умолчанию выводятся в концевых сечениях упругой части (начальном и конечном) и в центре упругой части, а при наличии запроса пользователя и в промежуточных сечениях по длине упругой части стержня. Для пластинчатых, объёмных, осесимметричных и оболочечных элементов напряжения выводятся в центре тяжести элемента и при наличии запроса пользователя в узлах элемента.
Правила знаков для усилий (напряжений) приняты следующими:
Для стержневых элементов возможно наличие следующих усилий:
N - продольная сила;
M - крутящий момент;
MY - изгибающий момент с вектором вдоль оси Y1;
QZ - перерезывающая сила в направлении оси Z1 соответствующая моменту MY;
MZ - изгибающий момент относительно оси Z1;
QY - перерезывающая сила в направлении оси Y1 соответствующая моменту MZ;
RZ - отпор упругого основания.
Положительные направления усилий в стержнях приняты следующими:
для перерезывающих сил QZ и QY - по направлениям соответствующих осей Z1 и Y1;
для моментов MX, MY, MZ - против часовой стрелки, если смотреть с конца соответствующей оси X1, Y1, Z1;
положительная продольная сила N всегда растягивает стержень.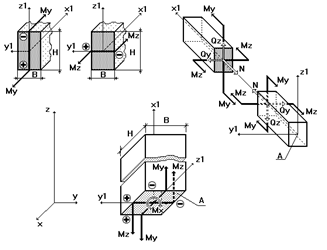
На рисунке показаны положительные направления внутренних усилий и моментов в сечении горизонтальных и наклонных (а), а также вертикальных (б) стержней.
Знаком “+” (плюс) помечены растянутые, а знаком ”-” (минус) - сжатые волокна поперечного сечения от воздействия положительных моментов My и Mz.
В конечных элементах оболочки вычисляются следующие усилия:
нормальные напряжения NX, NY;
сдвигающее напряжений TXY;
моменты MX, MY и MXY;
перерезывающие силы QX и QY;
реактивный отпор упругого основания RZ.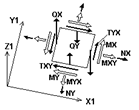
На рисунке показаны положительные значения напряжений, перерезывающих сил и векторов моментов, действующие по граням элементарного прямоугольника, вырезанного в окрестности центра тяжести КЭ оболочки.


В протоколе решения задачи для каждого из нагружений указываются значения суммарной узловой нагрузки, действующей на систему.
Значения расчетных сочетаний усилий представляютя в таблице результатов расчета «Расчетные сочетания усилий».
Вычисление расчетных сочетаний усилий производится на основании критериев, характерных для соответствующих типов конечных элементов - стержней, плит, оболочек, массивных тел. В качестве таких критериев приняты экстремальные значения напряжений в характерных точках поперечного сечения элемента. При расчете учитываются требования нормативных документов и логические связи между загружениями.
Основой выбора невыгодных расчетных сочетаний усилий служит принцип суперпозиции. Из всех возможных сочетаний, отбираются те РСУ, которые соответствуют максимальному значению некоторой величины, избранной в качестве критерия и зависящей от всех компонентов напряженного состояния:
а) для стержней - экстремальные значения нормальных и касательных напряжений в контрольных точках сечения, которые показаны на рисунке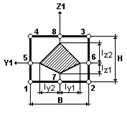
б) для элементов, находящихся в плоском напряженном состоянии - по огибающим экстремальным кривым нормальных и касательных напряжений по формулам: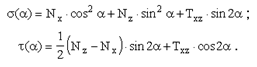
Обозначения приведены на рисунке. Нормальные напряжения вычисляются в диапазоне изменения углов от 90° до -90°, а касательные от 90° до 0°. Шаг изменения углов 15°.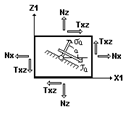
в) для плит применяется аналогичный подход - расчетные формулы приобретают вид:
Кроме того, определяются экстремальные значения перерезывающих сил.
г) для оболочек также применяется аналогичный подход, но вычисляются напряжения на верхней и нижней поверхностях оболочки с учетом мембранных напряжений и изгибающих усилий.
д) для объемных элементов критерием для определения опасных сочетаний напряжений приняты экстремальные значения среднего напряжения (гидростатического давления) и главных напряжений девиатора.
Задача устойчивости конструкции дымовой трубы решается в классической постановке для упругой системы и в предположении, что все приложенные к системе внешние нагрузки (следовательно, и внутренние силы) растут пропорционально одному и тому же параметру λ. То значение параметра λ, при котором матрица жесткости системы А(λ) впервые перестает быть положительно определенной, является критическим, а соответствующее значение λ - коэффициентом запаса устойчивости. Положительная определенность матрицы жесткости означает, что при любых значениях узловых перемещений и поворотов потенциальная энергия системы положительна, и для деформирования системы необходимо затратить энергию. В этом случае система в целом оказывает сопротивление деформированию (является отпорной). Если же система теряет устойчивость, она теряет отпорность и ее матрица жесткости становится вырожденной (с нулевым детерминантом).
Значения коэффициентов запаса устойчивости при комбинациях загружений представляются в таблице результатов расчета дымовой трубы « Коэффициенты запаса устойчивости от комбинаций».
При этом решается задача определения минимального λ, при котором происходит вырождение матрицы жесткости.
Поиск коэффициента запаса устойчивости проводится в интервале [0, 2.0], где 2.0 - оценка верхней границы интервала поиска коэффициента запаса устойчивости, которое задано в исходных данных. Если коэффициент запаса устойчивости системы больше указанной верхней границы, то он не вычисляется.
При составлении матрицы устойчивости для каждого конечного элемента (способного, в принципе, терять устойчивость) вычисляется значение λkp, которое приводит к потере устойчивости самого элемента в форме, когда все узлы, к которым этот элемент примыкает, остаются неподвижными. Номер элемента, на котором достигается min λkp, сообщается в протоколе.
Формы потери устойчивости от комбинаций представляется в таблице результатов расчета дымовой трубы «Формы потери устойчивости от комбинаций».
В предположении, что коэффициент запаса устойчивости является точным, найдено решение задачи о таких значений узловых перемещений и поворотов, которые вызываются только внутренними сжимающими напряжениями и усилиями. Это и есть форма потери устойчивости. Поскольку уравнение устойчивости решено при нулевой правой части, то форма потери устойчивости определена с точностью до множителя.
Формы колебаний конструкции дымовой трубы представляются в таблице результатов расчета «Формы собственных колебаний».
Для каждой из учтённых в динамическом загружении форм колебаний конструкции напечатана частота этой формы (круговые частоты w в радианах, частоты f в герцах, периоды колебаний Т в секундах). Они связаны зависимостями:![]()
Для каждой из учитываемых форм собственных колебаний напечатаны соотношения между величинами амплитуд в узлах расчетной схемы по каждой из разрешенных задачей степени свободы в узле. Наибольшая величина амплитуды назначается 1000, значения остальных величин амплитуд определяются в долях от 1000.
Инерционные нагрузки в узлах расчетной схемы по направлениям степеней свободы, разрешенных расчетной схемой, могут использоваться для анализа вклада каждой из учтенных форм собственных колебаний в прочностной расчет либо для дальнейших численных исследований конструкции. Для контроля выведено заданное распределение весов масс. Распределение весов масс указывает, например, как были распределены массы для собственного веса конструкции в указанные узлы сосредоточения.
Значения главных и эквивалентных напряжений в элементах конструкции дымовой трубы представляются в таблице результатов расчета «Главные и эквивалентные напряжения».
Значения главных и эквивалентных напряжений от комбинаций представляются в таблице результатов расчета «Главные и эквивалентные напряжения от комбинаций».
На проходящей через произвольную точку тела и произвольно ориентированной площадке, нормаль к которой v имеет направляющие косинусы l, m, n с осями x, y, z, действует нормальное напряжение sv и касательное напряжение tv с равнодействующей Sv.
Существуют три таких взаимно перпендикулярных площадки, на которых касательные напряжения равны нулю. На этих площадках, называемых главными, действуют главные напряжения s1, s2 и s3. При этом имеется в виду, что s1³s2³s3.Известно также, что главные напряжения обладают экстремальными свойствами, а именно - на любой площадке результирующее напряжение Sv£s1 и Sv³s3.
Для характеристики напряженно-деформированного состояния используется коэффициент Лоде-Надаи![]()
принимающий значение 1 при чистом сжатии, 0 при чистом сдвиге и -1 при чистом растяжении.
При выводе результатов расчета главные напряжения s1³s2³s3 обозначаются как N1³N2³N3 а для углов Эйлера введены обозначения: q - ТЕТА, y - PSI, j - FI.
Для плит и оболочек главные напряжения определяются на нижней (Н), срединной (С) и верхней (В) поверхностях. Положение главных площадок характеризуется углом наклона главного напряжения N1 к оси X1.
Главные напряжения в стержневых КЭ определяются по формуле![]()
Здесь sx, tx и ty нормальное и касательные напряжения в характерных точках контура поперечного сечения стержня.
Для сложного напряженного состояния, характеризующегося главными напряжениями s1, s2 и s3, обычно используется некоторая гипотеза (теория прочности), которая предусматривает возможность сопоставления некоторого эквивалентного напряжения se с пределом s0+, который соответствует простому одноосному растяжению. Условие, характеризующее отсутствие предельного состояния в материале, записывается в виде![]()
где k1,...,kn - некоторые константы материала. Иногда удобнее сопоставлять эквивалентное напряжение с пределом s0-, соответствующим сопротивлению образца материала при простом одноосном сжатии. Соответствующее эквивалентное напряжение обозначается как sS.
В расчете использовалась теория наибольших касательных напряжений:![]()